Aufgabe 2 - Das Energiefeld
Aufgabenstellung
Section titled “Aufgabenstellung”Aus Strategiespielen kennt man Ressourcenfelder, die Kristalle, Energie, o. ä. liefern. Erzeugen Sie nun Ihre eigene Spiellogik: Das Energiefeld startet mit 20 Energiepunkten. Pro Runde wächst es um 1 Punkt an (bis zu einem Maximum von 30 Punkten). Dies geschieht allerdings nur, solange das Energiefeld auch mindestens eine Kapazität von 1 hat. Sinkt die Zahl der Energiepunkte im Feld auf 0, vergehen 3 Spielrunden, bevor das Feld sich wieder wie gewohnt regeneriert.
Die „Energieextraktoren“ von drei unterschiedlichen Partien extrahieren nun die Energie dieses Felds. Jeder Arbeiter kann pro Runde bis zu drei Punkte Energie extrahieren. Pro Runde kann ein Extraktor am Feld arbeiten; die Extraktoren kommen „reihum“ zum Feld.
- Implementieren Sie die grundsätzliche Spiellogik.
- Implementieren Sie die Variante, in der die Extraktoren stets das Maximum (3 Punkte) nehmen.
- Plotten Sie den Gewinn und Energiewert über 10, 20 und 50 Runden.
- Analysieren Sie den Sachverhalt (Gefangenendilemma).
- Implementieren Sie eine Strategie zur Maximierung der sozialen Wohlfahrt.
1. Implementierung der Spiellogik
Section titled “1. Implementierung der Spiellogik”- Startenergie: 20.
- Regeneration: +1 pro Runde (Max 30), aber nur wenn Energie > 0.
- Erschöpfung: Wenn Energie auf 0 fällt, regeneriert das Feld für 3 Runden nicht (Cooldown).
- Extraktoren: 3 Stück, handeln nacheinander. Max Entnahme pro Extraktor: 3.
Die Simulation wurde objektorientiert in Python umgesetzt.
A) Das Energiefeld (class EnergyField)
Section titled “A) Das Energiefeld (class EnergyField)”Das Herzstück ist die Klasse EnergyField.Sie setzt den maximalen Energiestand (max_energy) und verwaltet den aktuellen Energiestand (energy) und den Cooldown-Timer (cooldown).
class EnergyField: def __init__(self): self.energy = 20 self.cooldown = 0 self.max_energy = 30Die Regenerations-Logik:
Hier muss beachtet werden, dass das Feld nur wächst, wenn der Cooldown inaktiv ist (cooldown == 0) und das Feld nicht leer ist bzw. das Maximum noch nicht erreicht hat.
def regenerate(self): # Fall A: Cooldown ist aktiv -> Runde abwarten if self.cooldown > 0: self.cooldown -= 1 return
# Fall B: Normales Wachstum (+1) bis zum Limit (30) # Voraussetzung: Es muss noch Energie im Feld sein (>0) if self.energy < self.max_energy: self.energy += 1Die Extraktions-Logik:
Beim Entnehmen wird geprüft, ob genug Energie vorhanden ist. Fällt die Energie durch die Entnahme auf 0, wird der Cooldown-Timer auf 3 gesetzt
def extract(self, amount_wanted): # Man kann nicht mehr nehmen, als da ist amount_taken = min(amount_wanted, self.energy) self.energy -= amount_taken
# Wenn das Feld leer ist -> 3 Runden Strafe (cooldown) if self.energy == 0 and amount_taken > 0: self.cooldown = 3
return amount_takenB) Der Spielablauf (run_simulation)
Section titled “B) Der Spielablauf (run_simulation)”Diese Funktion realisiert die Logik der drei Energieextraktoren. Sie steuert Runden (rounds) und sorgt dafür, dass die Extraktoren reihum auf das Feld zugreifen.
Mechanismen:
-
Reihenfolge: Mittels Modulo-Operator
(Runde - 1) % 3wird bestimmt, welcher der drei Spieler (Index 0, 1 oder 2) in der aktuellen Runde extrahieren darf. -
Strategie: Die Funktion akzeptiert einen Parameter, der festlegt, welche Entnahmemenge (
wanted) veruscht wird zu extrahieren. -
Zustand: Die Punkte der Spieler (
scores) werden nach jeder Runde akkumuliert und die Liste (history_total_score) gespeichert, genauso wie der Stand des Energiefeld (history_energy.append(feld.energy)).
def run_simulation(rounds, wanted): feld = EnergyField() history_energy = [] history_total_score = [] scores = [0, 0, 0] # Punktekonten der 3 Spieler
for r in range(1, rounds + 1): # 1. Feld regeneriert sich vor der Runde feld.regenerate()
# 2. Extraktion durchführen (nimmt max. 'wanted' oder Rest) got = feld.extract(wanted)
# 4. Gewinn dem aktuellen Spieler gutschreiben (Reihum-Logik) player_idx = (r - 1) % 3 scores[player_idx] += got
# 5. Zustand für Auswertung speichern history_energy.append(feld.energy) history_total_score.append(sum(scores))
return history_energy, history_total_score2. Variante mit Maximum
Section titled “2. Variante mit Maximum”In dieser Variante versuchen die Extraktoren/ Spieler immer, das Maximum von 3 Punkten zu erhalten bzw. weniger, wenn das Energiefeld nicht mehr liefern kann.
Das ist sichergestellt durch amount_taken = min(amount_wanted, self.energy) in der Extraction-Funktion.
Die Zeile min(3, 2) entscheidet sich immer für die kleiner Zahl.
Die Logik innerhalb der Simulationsschleife sieht so aus:
# Strategie "Maximum"def run_simulation(rounds, wanted): ... for r in range(1, rounds + 1): ... got = feld.extract(wanted)
run_simulation(rounds, 3)3. Simulation und Plotting
Section titled “3. Simulation und Plotting”Wir lassen die Simulation über 50 Runden laufen. Dies deckt auch die kürzeren Zeiträume (10, 20 Runden) im Verlauf ab.
Da es Zwei Zustände des Energiefeldes gibt (Vor- und Nach der Entnahme), passen wir die Funktion def run_simulation(rounds, wanted): leicht an und teilen history_energy in vor (pre) und nach (post) auf.
Zusätzlich werden die Start-Werte in der run_simulation Funktion direkt vor Runde 1 gesetzt
history_energy_pre = [feld.energy]history_energy_post = [feld.energy]history_total_score = [sum(scores)]Hier ist der Code für die Simulation:
import matplotlib.pyplot as plt
class EnergyField:def **init**(self):self.energy = 20self.cooldown = 0self.max_energy = 30
def regenerate(self): # Fall A: Cooldown ist aktiv -> Runde abwarten if self.cooldown > 0: self.cooldown -= 1 return
# Fall B: Normales Wachstum (+1) bis zum Limit (30) # Voraussetzung: Es muss noch Energie im Feld sein (>0) if self.energy < self.max_energy: self.energy += 1
def extract(self, amount_wanted): # Man kann nicht mehr nehmen, als da ist amount_taken = min(amount_wanted, self.energy) self.energy -= amount_taken
# Wenn das Feld leer ist -> 3 Runden Strafe (cooldown) if self.energy == 0 and amount_taken > 0: self.cooldown = 3
return amount_taken
def run_simulation(rounds, wanted): feld = EnergyField() scores = [0, 0, 0] # Punktekonten der 3 Spieler history_energy_pre = [feld.energy] history_energy_post = [feld.energy] history_total_score = [sum(scores)]
for r in range(1, rounds + 1): # 1. Feld regeneriert sich vor der Runde feld.regenerate() history_energy_pre.append(feld.energy)
# 2. Extraktion durchführen (nimmt max. 'wanted' oder Rest) got = feld.extract(wanted)
# 4. Gewinn dem aktuellen Spieler gutschreiben (Reihum-Logik) player_idx = (r - 1) % 3 scores[player_idx] += got
# 5. Zustand für Auswertung speichern history_energy_post.append(feld.energy) history_total_score.append(sum(scores))
return history_energy_pre, history_energy_post, history_total_score
# --- Main Ausführung ---rounds = 50wanted = 3e_pre, e_post, s_hist = run_simulation(rounds, wanted)# Wir erstellen eine Liste von 1 bis 50 für die X-Achsex_achse = list(range(0, rounds + 1))
# Plot erstellenplt.figure(figsize=(10, 10))
# Hier definieren wir, welche Runden wir beschriften wollenmark_rounds = [10, 20, 50]
# Subplot 1: Energieplt.subplot(2, 1, 1)# Linie 1: Vor der Ernte (Das Angebot)plt.plot( x_achse, e_pre, label="Verfügbar (Vor Ernte)", color="green", alpha=0.5, linestyle="--",)# Linie 2: Nach der Ernte (Der Rest)plt.plot(x_achse, e_post, label="Rest (Nach Ernte)", color="red", linestyle="--")plt.title("Zustand des Energiefeldes")plt.ylabel("Energie")# Wir setzen die X-Achse so, dass nur ganze Zahlen in 5er Schritten angezeigt werdenplt.xticks(range(0, rounds + 1, 5))plt.xlim(0, rounds) # Begrenzt die Ansicht exakt auf Runde 1 bis 50# Y-Achse Einstellungenplt.ylim(0, 32) # Hartes Limit unten (0) und oben (32, damit Platz für die 30 ist)plt.legend()plt.grid(True)
# Subplot 2: Gewinnplt.subplot(2, 1, 2)plt.plot(x_achse, s_hist, label="Summe Gewinn", color="red", linestyle="--")# MARKIERUNGEN FÜR GEWINNfor r in mark_rounds: y_val = s_hist[r] plt.plot(r, y_val, "o", color="black", markersize=4) plt.annotate( f"{y_val} Pkt", xy=(r, y_val), xytext=(r - 2, y_val + 5), # Text etwas links darüber arrowprops=dict(facecolor="black", arrowstyle="->"), ha="center", )plt.title("Akkumulierter Gewinn aller Spieler")plt.ylabel("Punkte")plt.xlabel("Runden")# Wir setzen die X-Achse so, dass nur ganze Zahlen in 5er Schritten angezeigt werdenplt.xticks(range(0, rounds + 1, 5))plt.xlim(0, rounds) # Begrenzt die Ansicht exakt auf Runde 1 bis 50# Y-Achse Einstellungenplt.ylim(bottom=0) # WICHTIG: Zwingt die Y-Achse, exakt bei 0 unten anzufangen!plt.legend()plt.grid(True)plt.tight_layout()plt.savefig("plot_energy.png")print("Plot gespeichert als plot_energy.png")Ergebnis
Section titled “Ergebnis”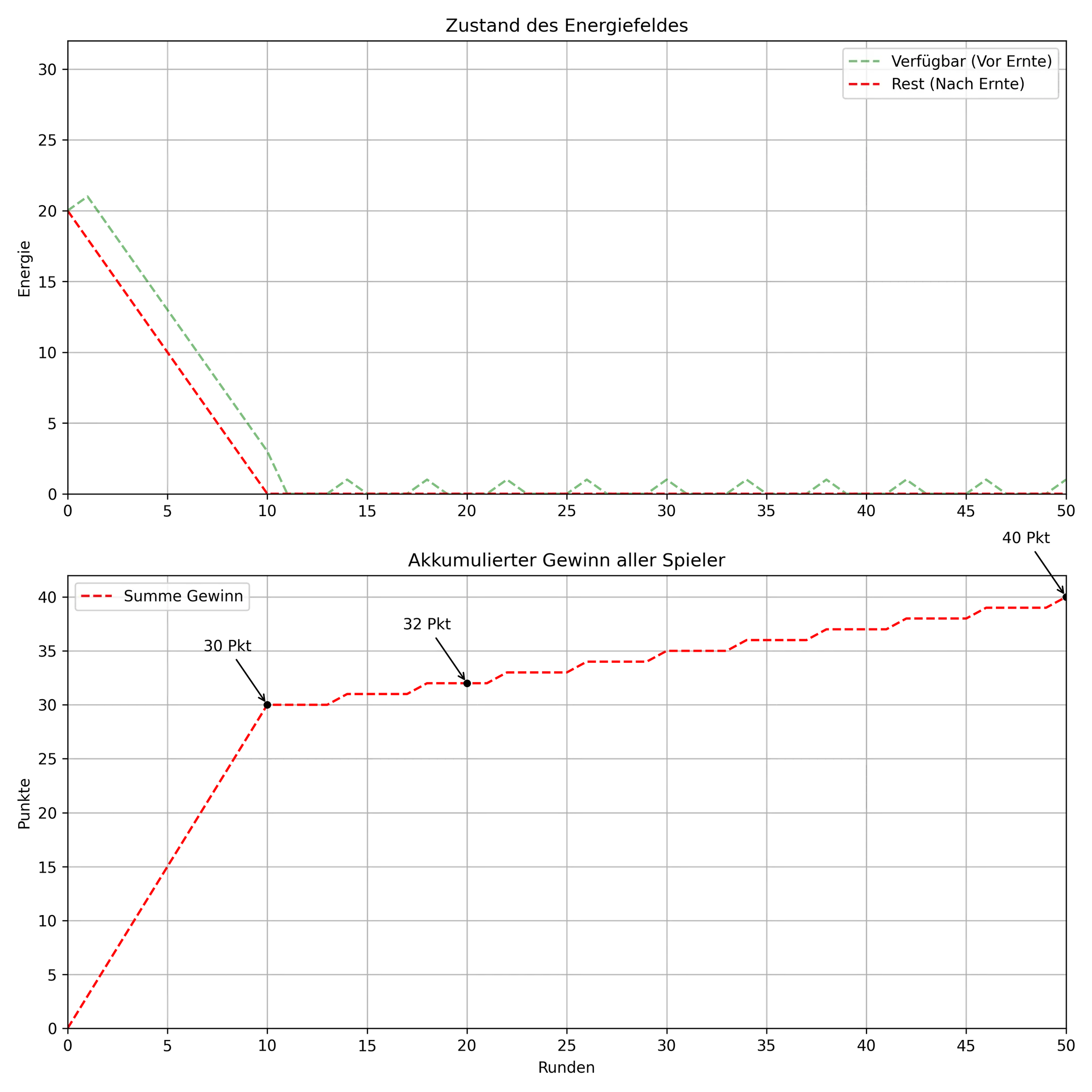
4. Analyse der Ergebnisse
Section titled “4. Analyse der Ergebnisse”Welcher Sachverhalt liegt vor?
Section titled “Welcher Sachverhalt liegt vor?”Die Ergebnisse der Simulation beschreiben den klassischen Sachverhalt der Tragik der Allmende.
Analyse Simulation:
Die Extraktoren “ernten” innerhlab der ersten 10 Runden das Energiefeld leer (auf 0), da sie immer versuchen das Maximum von 3 Punkten zu enthnehmen. Dadurch wird das Energiefeld überlastet, kommt mit der Regeneration nicht mehr nach, und wird auf Cooldown gesetzt und für 3 Runden unbrauchbar. Das Endergebnis (40 Punkte) könnte weitaus mehr sein wenn das Energiefeld nicht überlastet werden würde.
Allgemeine Beschreibung:
Die Tragik der Allmende beschreibt eine Situation, in der mehrere unabhängige Personen eine gemeinsame Ressource die “Allmende” (in unserem Fall das Energiefeld) nutzen. Jede Person handelt für sich genommen rational und gewinnmaximierend, indem sie versucht, so viel wie möglich von der Ressource zu konsumieren (Maximum von 3 Punkten).
Das Problem dabei ist: Wenn alle Nutzer so handeln, wird die Ressource übernutzt und schließlich zerstört (Cooldown Bestrafung). Das kurzfristige Verlangen nach eigenem Vorteil führt also langfristig zum Nachteil für die gesamte Gemeinschaft – und damit auch für jeden Einzelnen.
Zusammenhang mit dem Gefangenendilemma
Section titled “Zusammenhang mit dem Gefangenendilemma”Ja, es besteht ein direkter und starker Zusammenhang mit dem Gefangenendilemma.
Das Gefangenendilemma ist ein Modell welches aufzeigt, warum zwei (oder mehr) rational handelnde Personen oft nicht zusammenarbeiten, selbst wenn es im Interesse aller wäre.
Zusammenhang im Detail:
- Die Wahl: Jeder Spieler/Extractor hat die Wahl zu Kooperation (nur 1 Punkt nehmen um das Feld zu schonen) und Defektion (3 Punkte nehmen und gierig sein).
- Der Konflikt:
- Würden alle Zusammenarbeiten, wäre das Feld nie auf Cooldown und die Gesamtpunkzahl wäre weitaus höher.
- Ein einzelner Spieler hat den Anreiz zu “betrügen”: Wenn die anderen sparsam sind und nur 1 nehmen, kann er selbst 3 Punkte nehmen um sich einen Vorteil zu verschaffen
- Da jeder Spieler befürchtet, dass die anderen “betrügen” könnten (und er dann leer ausgeht, wenn er sparsam ist), entscheidet sich jeder Rational für die 3 Punkte.
- Das Ergebnis (Nash-Gleichgewicht): Alle Spieler wählen die 3 Punkte Strategie. Das führt zu einem Zustand, in dem sich keiner traut, seine Strategie einseitig zu ändern, obwohl das Gesamtergebnis für alle schlecht ist (das Energiefeld ist auf Cooldown).
Zusammenfassung
Section titled “Zusammenfassung”Zusammenfassend ist die Tragik der Allmende die wirtschaftliche/ökologische Konsequenz (Ressource kaputt/ Cooldown), während das Gefangenendilemma die spieltheoretische Entscheidungsstruktur beschreibt, die zu diesem Ergebnis führt.
5. Implementierung einer alternativen Strategie
Section titled “5. Implementierung einer alternativen Strategie”Anstatt immer 3 Punkte zu “ernten” und das Energiefeld zu überlasten ist die Strategie der Sozialen Wohlfart (die Summe der Gewinne aller Extraktoren dauerhaft zu maximieren) ein weitaus nachaltigerer Ansatz.
Dazu muss der Cooldown des Energiefeldes verhinder werden. Das Problem hierbei ist, dass die Entnahmerate (3) die Regenerartionsrate (1) übersteigt.
Die optimale Strategie lautet daher Nachhaltigkeit durch Kooperation: Die Extraktoren beschränken ihre Entnahme auf genau den Betrag, der pro Runde nachwächst.
- Regeneration: +1 pro Runde.
- Entnahme: 1 pro Runde.
- Netto-veränderung: 0 (Der Bestand des Feldes bleibt erhalten).
Implementierung
Section titled “Implementierung”Es muss lediglich beim Aufrufen der Simulationsfunktion der Parameter wanted von 3 auf 1 gesetzt werden:
# --- Main Ausführung ---rounds = 50wanted = 1 # nur 1 Energie "ernten"e_pre, e_post, s_hist = run_simulation(rounds, wanted)Ergebnis
Section titled “Ergebnis”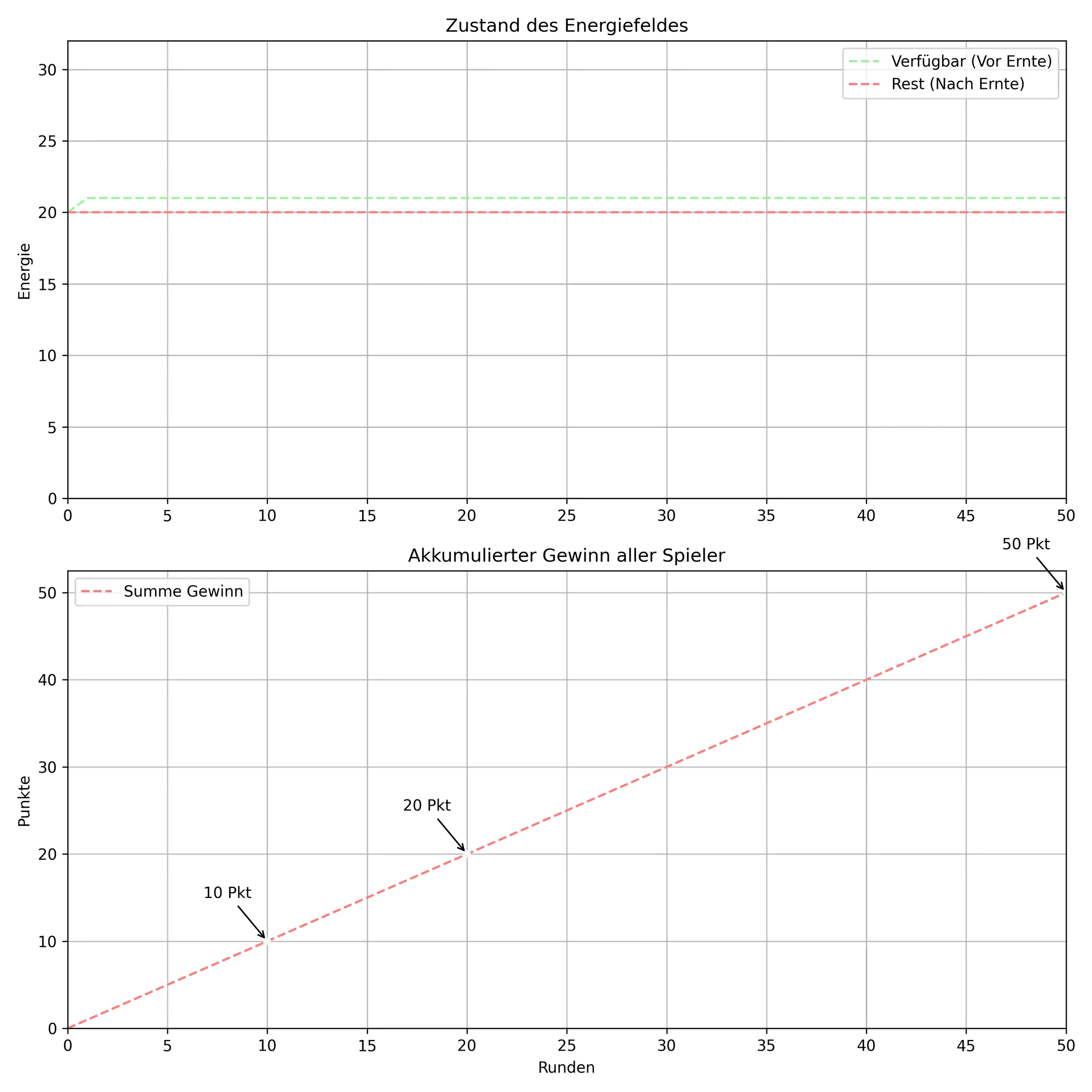
Ergebnis-Analyse
Section titled “Ergebnis-Analyse”Vergleichen wir die Ergebnisse nach 50 Runden:
- Gierig (Defektion): Das Feld bricht zusammen. Durch die ständigen Cooldown-Strafen erreichen die Spieler gemeinsam nur ca. 40 Punkte.
- Sozial (Kooperation): Das Feld liefert jede Runde verlässlich einen Punkt. Es treten keine Strafzeiten auf und das Energiezustand wird sich selbst bei unendlich weiteren Runden halten.
Damit ist gezeigt, dass die Maximierung der sozialen Wohlfahrt nur durch eine Anpassung der Entnahme an die natürlichen Grenzen der Ressource möglich ist.
Zusatz
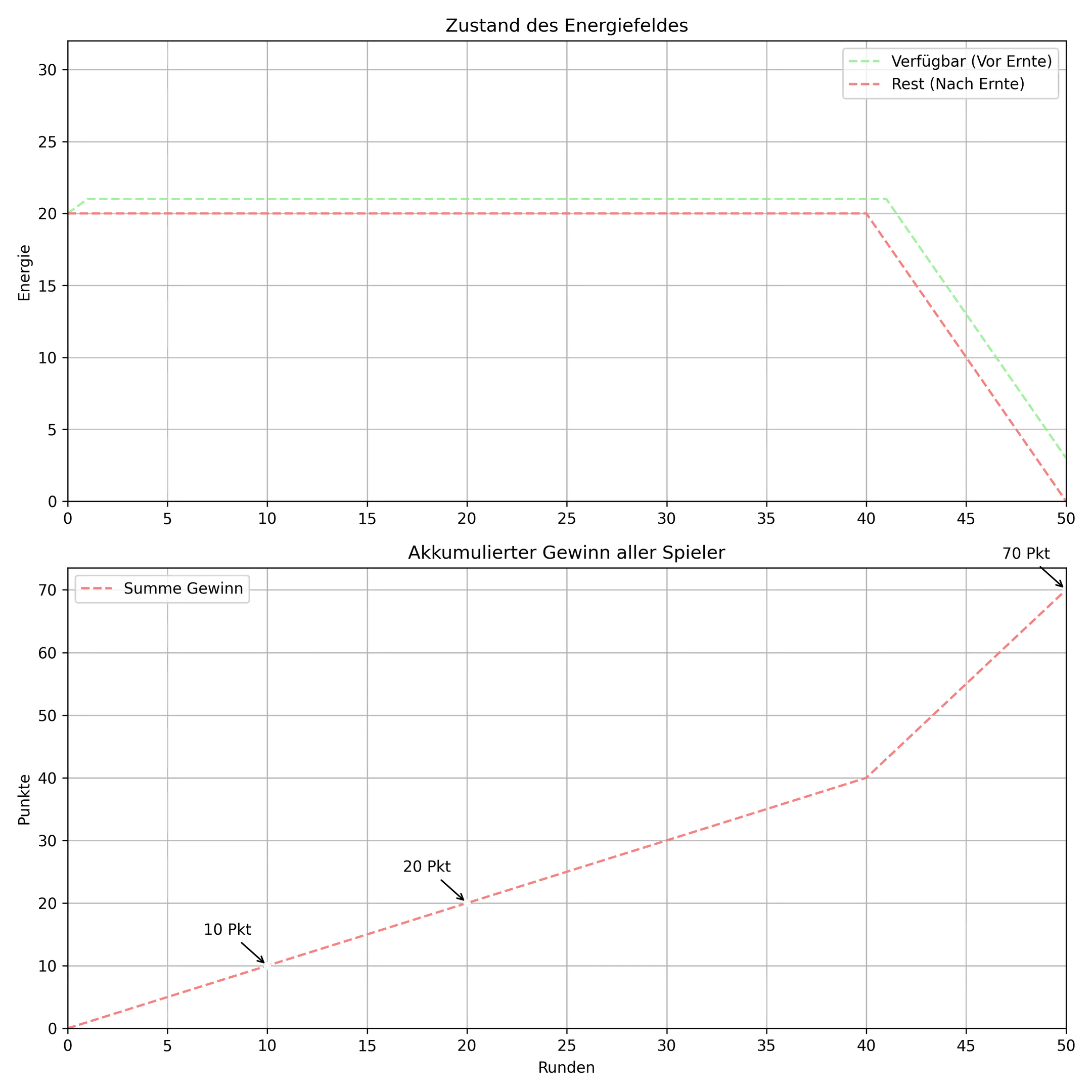
Section titled “Zusatz”Wenn man davon ausgeht, dass das Spiel nach 50 Runden vorbei ist und der Zustand des Feldes dann keine Relevanz mehr hat. Ist es sogar möglich einen noch höheren Maximalen Gewinn zu erreichen.
Wir wissen durch Aufgabe 2, dass die 3 Extraktoren das Feld, bei der gierigen (3 Punkte) entnahme, von 20 auf 0 Punkte innerhalb von 10 Runden Leer ernten.
Wenn wir nun die Nachhaltige Strategie der 1 Punkte entnahme bis zur runde 40 vortführen und dann in den letzten 10 Runden das Feld nochmal komplett leer ernten, durch eine 3 Punkte entnahme, würden wir das Maximal mögliche herausholen.
Simulations Maximum: